【素人が書く】scikit-learn を使って決定木学習 Pythonを添えて

この記事では、できるだけ詳しく説明をつけながら、手軽に学習を実行できる"Python scikit-learn を使って決定木学習"をやっていきたいと思います。

決定木を用いた分類は、分類されたデータの得られた結果の意味を理解しやすいか(意味解釈可能性)に配慮する場合に魅力的なモデルです。このモデルでは、データの特徴区間を矩形(角が直角になるような形)に分割することで、データの決定境界を構築するために、データに対していくつかの質問(分類基準)を行い、その結果からそれぞれどのクラスラベルに含まれるかを判断し、データを分類します。

といっても、わかりにくいので、図で極端に書くと以下のような感じです。

ここでは、私の大学に居るような大学生を例に描いています。

　　　　　　　

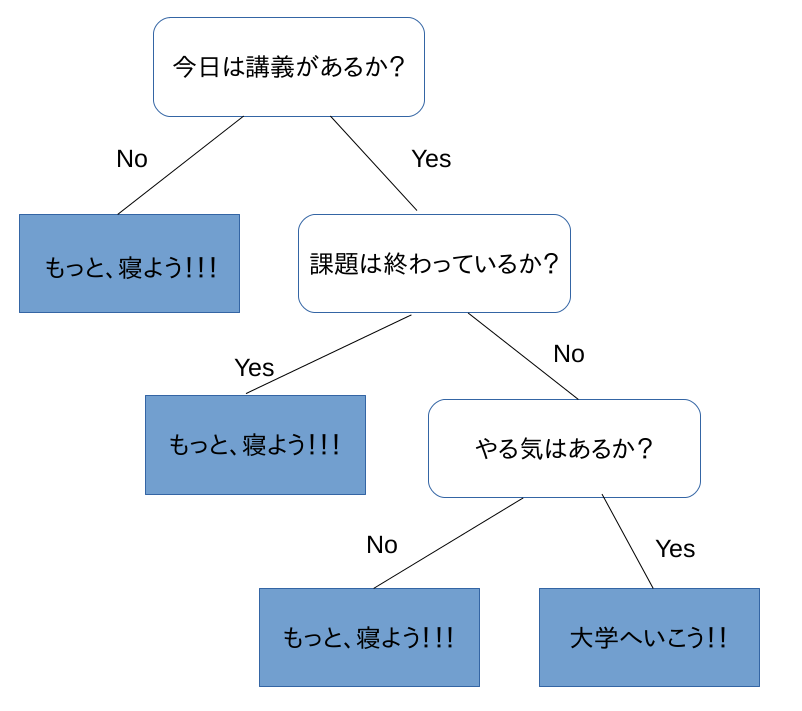
大量の大学生から、データをとり、そこから作成した決定木分類器が上のようにあるとします。

例えば、学生Aくんは、[今日は講義がある|課題は終わっている|やる気はない]の条件を持つとします。この場合、Aくんはrootの"今日は講義があるか？"から判別にかけられて、1段階目では、講義があるので、次の"課題は終わっているか"の2段目の子ノードへ流れます。Aくんは課題は終わっているので、ここでは、"もっと、寝よう！！！"の子ノードへ移動します。

この結果から、Aくんは、本日は"もっと、寝よう！！！"に分類(予想)されます。これが、人の行動予測であれれば、1日中寝る日と分類されたわけです。
　そんなの、寝るべき一択だろ！！

ここで、決定木学習の 過学習 落とし穴に触れておきます。
(以下、過学習の説明なので読み飛ばしてもらっても構いません)

決定木学習では、データサンプルから決定木を作成するのですが、例えば、先ほどの例では、質問が3つと少ないですよね？ また、その質問に対しての答えも2つしか(1つの親ノードあたりに子ノードが2つしか)ないです。
大学生の中には意識高い人であれば、講義や課題がなくても大学に行く人、寝るだけではなく、もっとサークルやバイトなど様々な人が居ると思います。そのような人をこの分類器にかけるとうまく分類出来ませんね。

では、このような人たちもデータサンプルとして決定木作成を行うことを考えましょう。

決定木の親ノードでの判別にはデータの持つ特徴量の大小などで判断します。では、データサンプルが100人分10項目のデータがあったとしましょう。このデータで決定木を作成するとして完全にフィットした決定木を作成すると、1段目のrootで複数個の子ノードが作成され、その子ノードそれぞれで、更に複数個の子ノードが作成される。このようなことが連鎖的に行われ、結果として決定木が非常に大きなものとなります。これでは、決定木を作成するのに非常に時間がかかりますし、データが完全に別れてしまうので、関連性など人間が見て分かるものが少ないのです。

更に、その決定木に未知のデータを通した時、学習用のデータセットに例がなければうまく分類することが出来ないことも挙げられます。

このように、決定木によって学習用のデータセットに対してはほぼ100%の精度で分類することが、未知のデータに対してはうまく分類が出来ない状態を 過学習 といいます。
過学習は多くの場合で、好まれない状況です。

もちろん過学習を防ぐことは、学習用のデータセットの分類精度を100%から下げる 代わりに、未知のデータの分類精度を上げる ことになりますが、現実には未知のデータに対しての評価を行うことがほとんどなので、むしろ未知のデータに柔軟に対応でき、分類精度を高める方が望ましいと基本的にはされています。

では、前置き・過学習に関してはこのあたりまでとして、 そろそろ実際にやっていきましょう。

今回使用するライブラリは以下の3つです。

• scikit-learn (1.18.1)
• matplotlib (2.0.0)
• myplot (自作)

まず、実装したプログラムは以下のものです。

3-6.py

では、コードをおおまかに解説します。

1〜7行目：使用するライブラリについて記述しています。ここで7行目に、"myplot"という見慣れないものがありますね。これは、自分で作成したライブラリmyplot.pyを使用しています。ここで詳しく実装内容については説明しませんが、このライブラリでは、 結果データをプロットしているもの と理解していただければそれだけでOKです。
更に、ここでは、題にもなっている scikit-learn の tree を用いていることも重要です。

11〜13行目：ここでは、使用する分類器作成に使用するトレーニングデータ と、そのトレーニングされた分類器にかけるテストデータをirisから整形しています。 12, 13行目をもっと具体的に説明すると、12行目では、irisのデータセットの中から、データラベル(X)とクラスラベル(Y)を取り出しています。13行目では、train_test_split()を用いて、X,Yの中からランダムに0.3:0.7[train:test]の割合でトレーニングデータとテストデータを分割しています。
まとめると

• x_train, y_train：データラベルX,クラスラベルYの分類器作成のためのトレーニングデータ
• x_test, y_test：データラベルX,クラスラベルYのテストグデータ

です。ちなみに、Xは 2×150データ([x0,y0], [x1,y1],・・・,[x149,y149])で、YにはXの列分に対応するクラスラベルが150個入っています。また、Yはクラスラベル(0,1,2)の3値を取ります。

16〜17行目：ここでは、具体的に決定木学習を行う際の設定をDecisionTreeClassifier()に対しておこなっています。この引数について少し説明しようと思います。第一引数では、決定木学習の分岐指標を設定しています。Treeは親ノードから子ノードに分岐するような形態を取るのですが、どのような条件で分岐するのか？をここでは平均情報量である"entropy"を用いています。この分岐条件には他にも、ジニ分散指標 などいくつかあるので、詳しくは公式ページを参照してくだい。次に第二引数(max_depth)では、作成される木の深さ(レベル)を設定しています。今回ではレベルは3で設定しています。この値ももちろん変更することができ、データ数を超えないほどに大きな値にすればある程度精度は良くなります。かといって、大きすぎる値になるとあまりうまくいきません。このことに関しては後の実行結果あたりで記述します。第三引数のrandom_state()では、内部で使用する乱数についてのseed値の設定です。17行目では、先ほどの設定にトレーニングデータを通して決定木を作成(学習)させています。更に、本来であれば、ここではテストデータのみを通せばいいのですが、あえて全データX, Yをそのまま通します。

18〜22行目：ここでは、決定木学習器に通したデータを描画しています。それだけです。

24行目：ここでは、分類したデータをより見やすく描画できるように".dot"ファイルで出力しています。後の実行結果でどのように使用されているのか説明・可視化しているので詳しくはそちらで。

ではでは、コードの説明もこのへんとして、ここからは実際の実行結果について書いていきます。

3-6.py を実行した結果、以下のようなグラフと、24行目で出力設定した"tree.dot"のバイナリファイルができます。

データラベルXの要素、( width, length)からなるグラフで、単に横軸：width, 縦軸：length であってそれが何かではなく、とりあえずその2つの要素からなるものと思ってください。

このグラフでは、色付けしてデータのラベル予測した範囲と、実データの様子を示しています。つまり、width の大きさにかかわらず、length が大体0.75以下であれば、赤色のラベルに分類されるということを示しています。青色、緑色も同様に読み取ることができます。

精度評価ですが、赤色の部分はうまく分類できていることがわかります。また、青色に関して一部緑色の領域に青色のマーカーがあることから、完全には分類できていないことがわかります。緑色からみた評価も同様です。

また、プログラムこのバイナリデータを25行目にあるコマンドで展開すると、以下のようなグラフが出力されました。

まず、16行目で設定している "max_depth=3"より、レベルが3で設定通り出力分類ができていることが ぱっと 見た感じでわかりますね。

一番上のレベル0ノードを見てみると、length が0.75以下であれば、赤色のノードの分類されることをここでは示しています。グラフの考察と一致してますね。正確には、平均情報量(entropy)の値に従って変化させた結果、そのように分類される結果となったと捉えます。

レベル1のノードでは、length が 4.95を基準に青色、緑色に分類されていることがわかります。本来では、この分類で、赤、青、緑 の3つのクラスラベルに分類されているので、いいように思えますが、このまま描画すると以下のようになってしまい、まだまだ上手く分類できてないことがわかります。

レベル2のノードでは、更に細かく、length, width の条件を追加するように分類されていることがわかります。この分割後の結果をグラフに表したものが最初にプロットされた図です。mat_depth=3 にした効果が出ていると実感できるのが、このレベル2のノードを見ると、緑色のノードから、緑色と青色の両クラスのノードが作成されていることがわかります。こればより細かく分割できているので制度的にお良くなった捉えることができ、今回ではmax_depth も 2 より 3 のほうが分類結果は良いとわかります。

実行は、異常なのですが、max_depth の値を大きくすれば精度が良くなるとすれば、どのくらいが妥当なのでしょうか？大きい値を使用するほど精度が良くなると言えるのでしょうか？

先に答えを述べるとそれは 99%No です。

まず、No の理由ですが、最初らへんで 過学習 について触れました。まさにここでは、過学習を起こしてしまう可能性があるので、max_depth が大きれば良いというのは一般的に正しいとは言えません。また、max_depth を大きくするということは、決定木が大きくなることを示し、結果として、過学習になるし、計算に時間かかるしで、あまり良いことはないと私は考えます。

99%の理由は何でしょうか？それは、場合によっては、うまくいこともあるのです。なので、可能性を残すような書き方をさせていただきました。しかし、一般的には良くはないです。

では、具体的にmax_depth はどのくらいに設定するのが良いのでしょうか？今回使用したのを例に説明します。まずは、max_depth = 4の図を載せます。

さぁ、どうでしょう。最下層ノードでは、青色から、青色、または、はっきりと分類できてない白色になりました。これはmax_depth=3 と比べてどうでしょう。私が考えるに、精度向上の可能性はあるがあまり意味のない分類と考えます。結果として、これをグラフ化しても、max_depth=3 と分類はほとんど変わらないグラフが出力されます。

先程も述べたように、計算量を増やしても、一つ前より大きな変化が見られない場合は、そのレベルでの計算は必要ないと私なら考えます。

実際、このmax_depthのような閾値をどこで引くのかが、技術者の腕でもあります。私の閾値の引き方も、人から見れば正しくないと捉えることもあります。みなさんがどのように引くのかは、ご自分で選んでください。私の引き方は参考程度にしてください。

なんか、堅苦しくなってしましましたが、今回はこのへんで、、、

非常に参考にさせていただきました。

Python機械学習プログラミング 達人データサイエンティストによる理論と実践 impress top gearシリーズ